How To Solve Number 75 For Animal Lines
| Pct - a special blazon of fraction | Percent Models | Ratios |
| Relationships:decimal fractions, mutual fractions, percentage and ratio | Rates | Quick quiz |
Percent - a special type of fraction
| | 0.25, 1/4, 25% These expressions tell us what portion of the foursquare is coloured orangish. |
The give-and-take percent come from the expression 'per cent' and literally means 'a part of one hundred'. A pct is a part, or fraction, out of 100. For example:
| 100% | =100/100 | =one | = 1.0 (decimal) | |
| 50% | = 50/100 | = 5/10 | = 1/2 | = 0.5 = 0.50 (decimal) |
| 25% | = 25/100 | = 5/20 | = one/4 | = 0.25 (decimal) |
| 40% | = 40/100 | = 4/ten | = 2/five | = 0.4 (decimal) |
| 5% | = five/100 | = 1/xx | = 0.05 (decimal) | |
| 0.5% | = v/yard | = 1/200 | = 0.005 (decimal) |
Nosotros can come across that to write a percent as a fraction nosotros express the percent equally a fraction with a denominator of 100. Nosotros may then be able to simplify the fraction further.
For example, 75% = 75/100 = 3/iv
To express a fraction equally a percent nosotros must offset convert the fraction into hundredths (in simple cases we can do this by using equivalent fractions) and and then supplant '/100' by the percent '%' sign.
For example, 4/five = eighty/100 = 80%
Nosotros can see that we limited a pct as a decimal by dividing by 100.
For example,
| 25% = 25/100 = 0.25 (xx-five hundredths) |
| 47.3 % = 47.3/100 = 0.473 (forty seven hundredths and 3 thousandths) |
| 200% = 200/100 = 2 |
To express a decimal every bit a per centum we multiply the decimal number by 100.
For example,
| 0.108 = 0.108 x 100 = 10.8% |
| 0.75 = .75 10 100 = 75% |
| i.2 = 1.2 x 100 = 120% |
Some percents expressed as fractions and decimals
| | | = 0.125 (decimal) |
| | | = 0.236 (decimal) |
| | | = 0.333 (decimal, rounded to 3 decimal places) |
| | | = 0.5 = 0.50 (decimal) |
| | | = 0.667 (decimal, rounded to 3 decimal places) |
| | | = 1.one (decimal) |
| | | = 1.5 (decimal) |
| | | =2.0 (decimal) |
Case 1: 30 out of 50 apples in a box are also bruised to sell. What percent of apples cannot be sold?
| Working Out | Thinking |
| | 30 out of 50 apples are bruised. To represent 30/50 every bit a per centum we demand to find out how many apples out of 100 are bruised. By equivalent fractions we know that 30 out of 50 equals 60 out of 100, so 60% of the apples are hobbling. We could also say that, |
Example 2: Ryan spent 25 minutes in the depository financial institution, 11 minutes of which was spent waiting in a queue. What pct of time did he spend waiting in the queue?
| Working Out | Thinking |
| | Ryan spent 11 minutes out of 25 minutes waiting in a queue. To turn this into a pct nosotros are asking, 11 out of 25 minutes equals how many minutes out of 100 minutes? We tin encounter that 11 mins out of 25 mins equals 44 mins out of 100 mins by equivalent fractions (because we know 25 x iv = 100) . Nosotros can say that Ryan spent 44%, 0.44 or 11/25 of his time in the bank waiting in a queue. |
Case iii: What per centum is 7 cm of 20 cm?
| Working Out | Thinking |
| | To find out what percent seven out of xx is, we need to enquire: 7 out of twenty is how many out of 100? v groups of 20 make 100, then seven out of 20 is 35 out of 100 (5 10 7 out of 5 x 20). Therefore 7/xx equals 35%, or 0.35 if we stand for information technology equally a decimal. |
![]()
Percentage models
Dual-calibration number line model
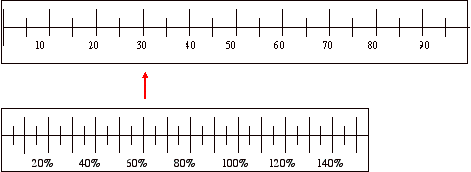
We can utilise the dual-scale number line, also called the proportional number line, to illustrate case ane from above.
| Recall case ane: xxx out of fifty apples in a box are too bruised to sell. What per centum of apples cannot be sold? | |
| Thinking | |
| The left side of the number line below has a per centum scale. The right side of the number line has a number calibration. Nosotros can characterization each scale using the information we are given in the problem. | Nosotros know that there are 50 apples in total, ie. 50 apples equals 100% of the apples. We know that 30 out of the 50 apples are bruised and we demand to find what percent this is. In more complicated problems this dual-scale number line is a practiced way of organising the information we are given and to piece of work out what information we demand to find. One time we take represented the trouble in this way we can write a proportion equation directly from the number line. xxx/50 = ?/100 Past equivalent fractions we know that 30/50 = 60/100. (Or we might accept just noticed that it is a 'multiply by 2' relationship, so xxx ten 2 = 60) Therefore lx% of apples are too bruised to sell. |
The dual-scale number line model is discussed further in the other pages of the Percent, Ratio and Rates topic.
Rubberband record measure model
The tape measure out model is a good linear model of percentage. Teachers can hands make these models using a ruler, such as a one metre ruler, and elastic. The elastic needs to be marked with a per centum scale. It can then be stretched to the desired length.
For example, what is threescore% of fifty?
To find the answer we line upward the zeros of the ruler and the elastic. We and so stretch the elastic so that 100% lines up with the whole amount, which in this case is fifty. We then look for 60% on the rubberband and read the corresponding amount on the ruler. We tin can see below that lx% of l is 30.
The intention is NOT to utilise this model accurately. It is a expert way of showing that percentage always involves a proportional comparing of something to 100.
1 metre ruler
Elastic
By manipulating the tape measure, this model can be used for the 3 types of percent problems, discussed in Percent Examples. Examples of which are,
What is twenty% of 50?
What percent is 10 of 50?
30% of what number is xv?
(Notation: for a lesson, a instructor volition need elastics tape measures of various lengths, because the elastic can only be stretched - it cannot be shrunk).
(This elastic record measure out model was developed by J. H. Weibe)
![]()
Ratios
| | The ratio of 1 : three tells us the ratio of shaded : unshaded The ratio of three : 1 tells us the ratio of unshaded : shaded The ratio of 1 : 4 tells usa the ratio of shaded : whole |
A ratio is another manner of comparing quantities. Each quantity must be measured in the same units. An reward of ratios is that we can compare several things at once.
| scale on a map (every one cm on the map represents 10000 cm on the basis, every inch on the map represents 10000 inches on the ground) | ratio of blue to white paint is 1 : four |
| ratio of gears on a cycle viii : 16 : 24 8:16:24 teeth on each cog | ratio of number of girls to number of boys in class is 5 : ii |
Although ratios must have each quantity measured in the aforementioned units, the units are not fixed. 1 litre of blue paint to 4 litres of the white paint represents the same ratio as i tin of blueish pigment to four tins of white paint, or 1 bucket of blue pigment to four buckets of white pigment. This fact makes ratios very versatile to use in everyday situations.
The order in which a ratio is written is very of import. If we say the ratio of the number of girls to the number of boys is five:ii this is very unlike to saying the ratio of the number of girls to the number of boys is 2:5.
A ratio tin be written in different ways;
- in words - the ratio of the number of girls to the number of boys is 5 to ii, and this is the way we say it
- using a colon - number of girls : number of boys = v : 2
We must always talk about ratios in context. To say or write 5 : two, for example, has no meaning on its own.
Example iv: Allow's say I want to make the paint colour 'sky blue' and I know that the way to do this is to mix ane part blue with iv parts white. This means there is a ratio of blueish to white of 1:4. In this case 1 litre of blue to 4 litres of white, making 5 litres of heaven blueish paint.
| | |
| 1 blue : 4 white | 2 bluish : viii white |
To make double the quantity of paint I tin mix the blue to white as a ratio of 2:viii. This will brand the same colour. The ratios of i:4 and 2:8 are equivalent, and worked out in the same mode equally equivalent fractions. We multiply each part of the original ratio by the same number and nosotros tin find equivalent ratios.
| 1 : four | ane : 4 | ane : 4 | |||
| x 2 | x 3 | x4 | |||
| 2 : viii | 3 : 12 | iv : 20 |
Sharing quantities in a given ratio
Instance 5: We take a pocket-size inheritance of $15000 to be shared among 3 people in the ratio of 2 : two : 1, how much does each person receive?
| Working Out | Thinking | ||||||||||||
| The ratio of 2 : 2 : one ways that the inheritance is divided into 5 portions - 2 people each receive 2 portions and 1 person receives 1 portion. $15000 divided by 5 - each portion is worth $3000 |
![]()
Relationships - decimal fractions, common fractions, per centum and ratio
We can utilise examples to illustrate the relationships between decimal fractions, mutual fractions, percent and ratio.
Case six: An inheritance of $15000 is to be distributed amongst 3 people in the ratio of two : two : 1. ($15000 will be divided into five portions)
| Person 1 | Person 2 | Person three | |
| ratio | 2 : | two : | 1 |
| common fraction | | | |
| decimal fraction | 0.4 (of $15000) | 0.4 (of $15000) | 0.two (of $15000) |
| pct | 40 % (of $15000) | xl % (of $15000) | 20 % (of $15000) |
Case 7: Ratios and partial parts.
A litre of mixed cordial requires 250 mls of cordial and 750 mls of water. How can we stand for this as a ratio and a fraction?
| Thinking |
| The ratio of cordial to water is 250 : 750 or 1 : 3. One part cordial to 3 parts water. Nosotros talk virtually the ratio of cordial to water in many different ways: For every cup of cordial there are 3 cups of water. There is three times equally much water as cordial. 1 out of every 4 parts of the mixed cordial is cordial. Can y'all think of whatsoever more ways? |
Instance 8: Ratios and partial parts.
A group of 100 people is fabricated up of 60 males and 40 females. How tin can we represent this as a ratio and a fraction?
| Thinking |
| The ratio of males to females is 60 : 40 or vi : 4. This means that overall there is a college proportion of males in the group, and for every 6 males in that location are 4 females. In fraction terms, where we are talking virtually the group of 100 people, lx/100 (6/10) are male and xl/100 (4/ten) are female. Then we can likewise say that half dozen out of every 10 people are males and 4 out of every x people are females. Whereas fractions only enable us to represent the part to whole relationship (in this instance, males/people and females/people), different aspects of the relationships between quantities (people) tin be shown using ratios. For example, The three ratios that represent the relationships of males and females in this group of people are: - the ratio of 6 males to 10 people can be represented equally 6 : 10 - the ratio of 4 females to 10 people can be represented every bit 4 : 10 - for every vi males in that location are iv females can be represented as Which ratio we cull depends on nosotros want to say. The number of males to the number of females is 6 : 4 The number of males to the number of people is 6 : 10 The number of females to the number of people is 4 : 10 |
In the early stages of introducing ratio at a primary level nosotros by and large discuss ratios in terms of a part to part or, quantity to quantity, comparing. At this stage part to whole relationships are often amend represented past fractions or percents with which students already have some feel. When function to whole ratios are introduced care must be taken to ensure students clearly understand what is being represented.
![]()
Rates
Nosotros use rates when nosotros are measuring 1 quantity or amount in relation to another quantity or corporeality. We use them to compare how quantities change, normally over a period of fourth dimension. A significant difference between rates and ratios is that when we are forming rates, each quantity is measured in unlike units to form new composite units.
For case, permit's say y'all are travelling at a rate of 60 kilometres per hour (km/h). Here nosotros are measuring kilometres in relation to hours and the rate unit becomes 'kilometres per hour', oft written as km/h.
Other examples of rates are, an athlete running at 10 metres per second (m/s), and a factory using water at a rate of 450 litres per hour (l/h).
Some rates we commonly apply are:
| km/h | kilometres per hr |
| c/L | cents per litre |
| $/m | dollars per infinitesimal |
| c/m | cents per infinitesimal |
Example 9: A hose is running h2o at the abiding rate of 100 litres an hour.
1. How many litres volition run in ii hours?
2. How many hours will it take to run 350 litres?
| Working Out | Thinking |
| 100 litres/one 60 minutes = ? litres /2 hours 200 litres will run in 2 hours. | Nosotros know that 100 litres runs in one hour and we demand to find out how many litres runs in 2 hours. Nosotros tin write this every bit litres/60 minutes because this is what we are trying to notice out. |
| Working Out | Thinking |
| 100 litres/i 60 minutes = 350 litres /? hours 350 litres/ ? hours = 100 litres /i hour 350 litres/3.5 hours = 100 litres/1 hour | We know that 100 litres runs in 1 hr and nosotros need to know how long it takes to run 350 litres. |
![]()
Quick quiz
| 1. | Limited the following percents equally fractions and decimals: | ||||
| a) | 95% | ||||
| b) | 13.5% | ||||
| c) | 42% | ||||
| d) | 1% | ||||
| east) | 0.ane% | ||||
| 2. | Express the following fractions every bit percents: | ||||
| a) | 37/100 | ||||
| b) | 164/100 | ||||
| c) | 25/50 | ||||
| d) | 14/20 | ||||
| due east) | xvi/25 | ||||
| iii. | Express the post-obit decimals as percents: | ||||
| a) | 0.01 | ||||
| b) | 0.83 | ||||
| c) | 0.005 | ||||
| d) | 1.10 | ||||
| e) | 0.2 | ||||
| 4. | Express the following quantities as ratios: | ||||
| a) | There were 3 boys for every 5 girls at school assembly. | ||||
| b) | Ix people out of every ten watch television every nighttime. | ||||
| c) | In a class of 25 students 3 are left handed and 22 are right handed. | ||||
| d) | To cook rice you need 1 loving cup of rice to two cups of water. | ||||
| e) | To brand ANZAC biscuits, you lot add the same amount of flour to sugar. | ||||
| 5. | The following ratios of pets endemic take been obtained from surveys of five local neighbourhoods. Detect at least one equivalent ratio for each of the following: | ||||
| a) | dogs : cats = x : xx | ||||
| b) | cats : dogs = 30 : 50 | ||||
| c) | dogs : cats = 100 : 100 | ||||
| d) | dogs : cats : guinea pigs = vi : 4 : two | ||||
| e) | fish : turtles = 75 : 25 | ||||
| 6. | Express each part-to-part ratio below equally a common fraction, decimal fraction and a percentage of the whole: | ||||
| a) | men : women : children = iii : 3 : 4 | ||||
| b) | men : women : children = 11 : 4 : 5 | ||||
| c) | adults : children = 4 : 1 | ||||
| d) | men : women : children : pets = 5 : 3 : half-dozen : 1 | ||||
| 7. | Write each of these sentences as a rate: | ||||
| a) | She ran 100 metres in xv seconds. | ||||
| b) | The bus travelled 850 kilometres in 10 hours. | ||||
| c) | Ilana can type 160 words in 2 minutes. | ||||
| d) | The factory packaged 600 packets of biscuits in v minutes. | ||||
Extra questions:
Shade 20% of this diagram
(a) What percent of the following shape is shaded?
(b) What percentage is non shaded?
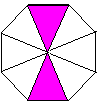
three. What is the ratio of pink to white in the following figure?
iv. A biro is 23 cm long and a ruler is 30 cm long.
(a) What is the ratio of the biro to the ruler?
(b) What is the ratio of the ruler to the biro?
5. Complete the following table.
| Percentage | Common Fraction | Decimal Fraction |
| 32% | ||
| 0.06 | ||
| |
6. A dog is iii times as long as a bird. The canis familiaris is 90 cm long.
(a) How long is the bird?
(b) Write a ratio to evidence the relationship of the canis familiaris to the bird.
7. I have a 300g handbag of sugar and a half a kilo of butter.
(a) What is the ratio of the sugar to the butter?
(b) What is the ratio of the butter to the saccharide?
eight. What two quantities are beingness measured when the units are km/hr?
To view the quiz answers, click hither.
![]()
Source: https://extranet.education.unimelb.edu.au/SME/TNMY/Arithmetic/percent/meaning/percentmean.html
Posted by: tarverwhers1980.blogspot.com


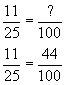
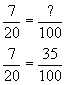
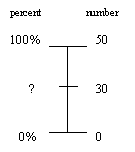



0 Response to "How To Solve Number 75 For Animal Lines"
Post a Comment